Module 2: Basic Concepts of Trigonometric Functions
Topics
After completing this section, you should be able to:
- find the six trigonometric function values of any acute angle of a right triangle
- determine the exact trigonometric function values of 30°, 45°, and 60° angles
- use a calculator to find trigonometric function values
- solve any right triangle by calculating its side and angle measurements
- use trigonometry to solve applied problems related to right triangles
The study of trigonometry begins by focusing upon the relationships between the sides and angles of right triangles.
First consider a brief review of terminology.
A triangle is a three-sided polygon.
Each pair of sides of a triangle has a common point called a vertex.
Each pair of sides forms an angle interior to the triangle.
Angles are often denoted by Greek letters
such as |
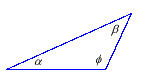 |
Angles are often measured in degrees. If a disk is cut into 4 equally sized wedges, each wedge contains an angle of 90 degrees. |
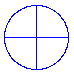
|
If a disk were cut into 360 equal wedges, each wedge would contain an angle of 1 degree. This idea of using 360 divisions originated with the ancient Babylonians, and it remains embedded in the current degree system of angle measurement.
A right angle is an angle whose measure is 90 degrees, denoted 90°, using the "°" symbol for "degrees." |
 |
| An acute angle is an angle whose measure is greater than 0° and less than 90°. |  |
| Two angles whose measures sum to 90° are called complementary angles. For example, the acute angles measuring 32° and 58° are complementary, since 32° + 58° = 90°. | 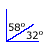 |
Recall that for any triangle, the sum of the measures of the three angles is 180°.
A right triangle is a triangle that contains a right angle. In a right triangle, since the sum of the three angles is 180° and one of the angles is 90°, the sum of the measures of the two remaining angles must be 180° – 90°, or 90°. Therefore, the two remaining angles in a right triangle are both acute and complementary.
Draw a right triangle and label the acute angles
The hypotenuse of the right triangle is the longest side, the side opposite the right angle. The other two sides are called legs of the triangle. |
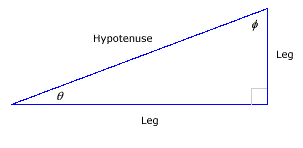 |
The legs can be labeled according to their relationship to the angle θ. One of the legs is the side opposite θ, and the other leg is referred to as the side adjacent to θ. | 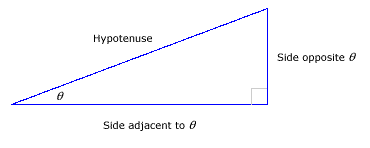 |
The ratios of the lengths of the sides are called trigonometric ratios, or trigonometric function values, of the angle θ. There are six ratios.
One of the ratios is the length of side opposite θ divided by the length of the hypotenuse. This ratio is called the sine of θ.
For the right triangle shown, sin θ
= 3/5 = 0.60 and This triangle is called the 3-4-5 triangle, since the lengths of the sides are 3, 4, and 5. |
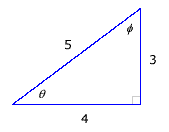 |
The other five ratios are called the cosine, tangent, cosecant, secant, and cotangent. The ratios are defined as follows:
| Trigonometric Function Values of an Acute Angle θ | ||||||
|---|---|---|---|---|---|---|
|
For the right triangle pictured, the set of six
trigonometric |
 |
|
|
|
|
|
|
|
|
|
| The set of six trigonometric ratios associated with angle
|
|
|
|
|
|
|
|
|
|
|
From the definitions and previous examples, it is easy to see that there are relationships among the trigonometric function values.
-
| The cosecant is the reciprocal of the sine. | |
| The secant is the reciprocal of the cosine. | |
| The cotangent is the reciprocal of the tangent. |
If you know the sine, cosine, and tangent of an angle, then by taking the reciprocals, you get the cosecant, secant, and cotangent.
There is a mnemonic aid that can help you to remember the definitions for the sine, cosine, and tangent ratios. Think of Professor SOH-CAH-TOA (pronounced phonetically as "soak a toe-a"). The joke is that the Professor is a wizard at trigonometry, but has a sore toe which needs to be soaked!
SOH-CAH-TOA is shorthand for |
Sine: Opposite/Hypotenuse |
For the example involving the 3-4-5 triangle, notice that the trigonometric ratios of angle
θ
are related to the trigonometric ratios of angle ![]() . For example, sin
θ = 3/5 = cos
. For example, sin
θ = 3/5 = cos
![]() and cos
θ = 4/5 = sin
and cos
θ = 4/5 = sin
![]() . Since angles
θ and
. Since angles
θ and
![]() are complementary,
are complementary,
![]() = 90° –
θ.
= 90° –
θ.
sin
θ = cos
![]() = cos (90° –
θ) and cos
θ = sin
= cos (90° –
θ) and cos
θ = sin
![]() = sin (90° –
θ).
= sin (90° –
θ).
Because of this relationship, the sine and cosine functions are called cofunctions. There are similar relationships between the tangent and cotangent, and between the secant and cosecant functions. These relationships are listed below.
Cofunction Identities
| sin θ = cos (90° – θ) | cos θ = sin (90° – θ) |
| tan θ = cot (90° – θ) | cot θ = tan (90° – θ) |
| sec θ = csc (90° – θ) | csc θ = sec (90° – θ) |
An interesting question to ask is this: For right triangles having the same proportions, does a larger triangle have larger trigonometric function values? To answer this, consider similar triangles.
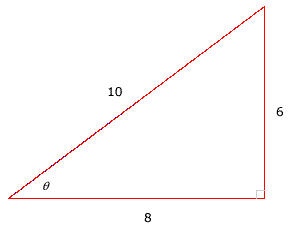
Recall that two triangles are similar if the corresponding angles have the same measure or—equivalently—the corresponding sides are proportional. For example, the 3-4-5 triangle and the 6-8-10 triangle are similar. Each side in the 6-8-10 triangle is twice as long as the corresponding side in the 3-4-5 triangle.
| 3-4-5 Triangle
|
6-8-10 Triangle
|
For the 6-8-10 right triangle, the set of six trigonometric ratios associated with angle θ are given by
|
|
|
|
|
|
|
|
|
The 6-8-10 triangle has the same trigonometric ratios as the 3-4-5 triangle.
An analogous result applies to any two similar triangles.
-
Given any two similar triangles, because the lengths of corresponding sides are proportional, the trigonometric ratios remain the same. The trigonometric ratios of θ depend on the measure of the acute angle θ, but not on the size of the triangle.
Recall that the Pythagorean theorem (module 1, topic I-B) relates the lengths of the three sides of a right triangle. The sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. |
 |
Given just one of the trigonometric ratios, it is possible to use the Pythagorean theorem to assist in determining the remaining five trigonometric ratios.
Callout
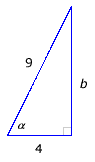
Example I.B.1: If cos ![]() = 4/9 and
= 4/9 and ![]() is an acute angle
of a right triangle, what are the remaining five trigonometric function values?
is an acute angle
of a right triangle, what are the remaining five trigonometric function values?
Solution:
Since
draw a right triangle whose hypotenuse has length 9. Label one of the acute angles |
 |
||||||
|
Use the Pythagorean theorem to find the length of the side opposite Now the lengths of all three sides are known, and the five remaining trigonometric function values can be determined:
|
|||||||
There are certain acute angles that appear very frequently in trigonometric applications: 30°, 45°, and 60°. It is worthwhile to compile a table of the trigonometric function values for these angles. Fortunately, it is relatively simple to derive the values, by using basic geometric facts and working with appropriate triangles.
Recall that an isosceles triangle is a triangle having two sides of the same length or—equivalently—two angles of the same measure.
For an isosceles right triangle, both acute angles must have measures of 45°, since the acute angles are complementary and have equal measure.
Take a square and cut it in half along a diagonal to get two isosceles right triangles. Pick one of the isosceles right triangles and label the legs and the hypotenuse.
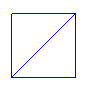
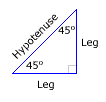
For convenience, suppose the legs each have length 1. Use the Pythagorean theorem to find the length of the hypotenuse:
Since 12 + 12 = c2, then 2 = c2 and the length of the
hypotenuse is![]() .
.
Now it is easy to determine the trigonometric function values of an angle of 45°.
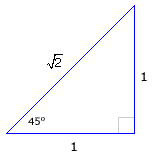 |
The remaining trigonometric function values can be determined by taking the reciprocals. |
Next, determine the trigonometric function values of 30° and 60°. Notice that if a right triangle contains an angle of 60°, then the other acute angle must have a measure of 30°, since the angles are complementary.
An equilateral triangle is a triangle having all three sides of the same length, or equivalently all three angles of the same measure. Because the sum of the measures of the three angles must be 180°, each angle in an equilateral triangle must measure 60°.
Take an equilateral triangle and cut it in half to get two right triangles.
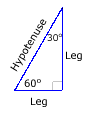
Each right triangle has acute angles 30° and 60°.
For convenience, suppose that the sides of the equilateral triangle have length 2. Then each right triangle has a hypotenuse of length 2 and a leg of length 1.
Use the Pythagorean theorem to find the length of the other leg:
12 + b2 = 22, so b2 = 3 and the length of
the other leg is![]() .
.
Now it is easy to determine the trigonometric function values for angles of 30° and 60°.
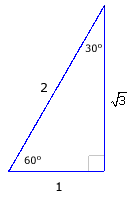 |
The remaining trigonometric function values can be determined by taking the reciprocals. |
The sine, cosine, and tangent function values of 30°, 45°, and 60° are summarized in the following table.
| Angle θ | sin θ | cos θ | tan θ |
|---|---|---|---|
| 30º | |||
| 45º |
|
|
1 |
| 60º |
|
For the 45° angle, it is good to keep in mind the 1-1-![]() triangle.
triangle.
For the 30° and 60° angles, it is good to keep in mind the 1-![]() -2 triangle.
The shortest side is the side opposite the 30° angle.
-2 triangle.
The shortest side is the side opposite the 30° angle.
By drawing and referring to the appropriate triangle, you can quickly derive the trigonometric function values without consulting the table.
Trigonometric function values of any angle can be found using a scientific or graphing calculator. Most calculators find values for the sine, cosine, and tangent, and the user finds the cosecant, secant, and cotangent by computing the appropriate reciprocal.
As you will see later on in topic III-A, there is more than one unit of measurement for angles. Be sure to put your calculator in degree mode (denoted DEG) when working with angles measured in degrees.
Callout
Example I.D.1: Find sin 37.5° and csc 37.5°, rounding the results to four decimal places.
Solution:
sin 37.5° ≈ 0.608761429, or 0.6088 when rounded to four decimal places.
csc 37.5° = 1/(sin 37.5°) ≈ 1.642679632, or 1.6427 when rounded to four decimal places.
Recall that very large numbers and very small numbers are often written in scientific notation. Many calculators display a letter E preceding the exponent. For example, a calculator display of 1.6520000E-03 represents 1.6520000 × 10-3 = 0.001652.
Callout
Example I.D.2: Find tan 0.03° and cot 0.03°, writing the values in scientific notation to four decimal places.
Solution:
tan 0.03° ≈ 5.235988234 × 10-4, or 5.2360 × 10-4 when rounded.
cot 0.03° = 1/(tan 0.03°) ≈ 1909.859143 ≈ 1.9099 × 103 in scientific notation.
So far, you have taken an angle and found a corresponding trigonometric value. Going from a trigonometric value to an angle is the inverse process. (Inverse trigonometric functions will be discussed in detail in module 3.)
A calculator can be used to carry out the inverse process, to find an acute angle that has a given trigonometric value. Typically, a calculator uses a SHIFT key or an INV key. Put your calculator into degree (DEG) mode. Enter the trigonometric value, press SHIFT (or INV), then the trigonometric function. (You may need to consult the instructions for your calculator.)
Callout
Example I.D.3: Find the acute angle whose cosine is 0.8391, rounding to 2 decimal places.
Solution:
The acute angle whose cosine is 0.8391 is approximately 32.95°.
| Consider a right triangle having legs of length a and b, a hypotenuse of length
c, and
acute angles
θ and
|
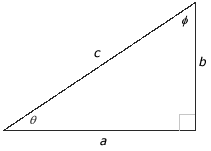 |
To solve a triangle is to determine the lengths of all three sides and the measures of all three angles. Solving a triangle is similar to solving a puzzle. There are six values to find.
In the case of a right triangle, one of the angles must have a measure of 90°, and the lengths of the sides are related by the Pythagorean theorem. So, with just a little more information, it is possible to solve the right triangle.
Callout
Example I.E.1: Solve the right triangle having a hypotenuse of length 15 and a leg of length 8.
Solution:
|
Draw and label a right triangle so that the hypotenuse is 15 and one of the legs is 8. Label the angles. Suppose θ is the angle whose opposite side has length 8. It is helpful to label the other acute angle and the third leg. Then at a glance, you can tell that in order to solve the triangle, you must determine the two angles and the length of the side adjacent to θ. Use the Pythagorean theorem to find the length of side a: |
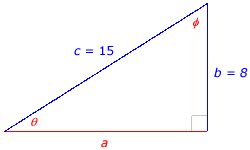 |
|
Since you know the lengths of the hypotenuse and the side opposite angle θ, the sine of θ can be determined: sin θ = 8/15 Using a calculator, find the acute angle θ whose sine is 8/15, which is approximately 32.2°. The measure of the other acute angle
The lengths of the three sides are 8, 15, and
|
|
Problem 2: Given a right triangle, suppose you know the measure of one of the acute angles and the length of one side. That is, you know one angle and the length of either the hypotenuse or the side opposite the angle or the side adjacent to the angle.
Callout
Example I.E.2: Solve the right triangle having an angle of 65.4° and opposite side of length 27.
Solution:
Draw a right triangle so that an acute angle is 65.4°, and the side opposite the angle has length 27. Denote the length of the side adjacent to the 65.4° angle by a, and the length of the
hypotenuse by c. Let
|
 |
Since one acute angle has measure 65.4°, the other angle
![]() has measure 90° – 65.4° = 24.6°.
has measure 90° – 65.4° = 24.6°.
Since the angle 65.4° is known and the length of the opposite side is known, the sine function can be used to find the length of the hypotenuse:
![]() , where
c is the length of the hypotenuse.
, where
c is the length of the hypotenuse.
Solve for c:
![]()
The tangent function can be used to find a, the length of the side adjacent to 65.4°:
![]()
Solve for a:
![]()
The lengths of the three sides are 12.36, 27, and 29.70. The measures of the angles are 24.6°, 65.4°, and 90°.
The branch of mathematics known as trigonometry arose from the need to solve real-world problems involving right triangles.
Applications often involve a horizontal line of reference. An angle measured above the horizontal line is called an angle of elevation. An angle measured below the horizontal line is called an angle of depression.
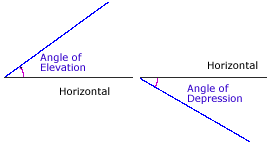
Callout
Example I.F.1: A monument and a building are 200 feet apart. At the top of the monument, the angle of elevation to the top of the building is 35°. If the monument is 80 feet high, how tall is the building?
 |
Callout
Example I.F.2: Aviation equipment aboard an airplane has determined that the distance from the plane to a radar station is 14.8 miles, and the angle of depression is 22°. If a car is parked on the ground directly below the plane's aviation equipment, how far is the car from the radar station? What is the altitude of the plane, in feet?
 |
After completing this section, you should be able to:
- determine the trigonometric function values of any angle in standard position
- use reference triangles, symmetry principles, and reference angles as aids in finding trigonometric function values
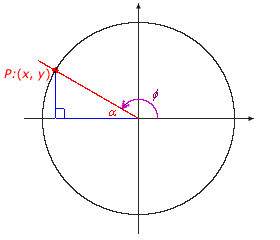
The notion of a trigonometric function can be extended to angles which are not acute angles. To describe a general angle, the angle is put in a frame of reference called standard position.
An angle consists of two rays having the same endpoint, called the vertex. One of the rays is placed along the positive x-axis with the vertex at the origin. This ray is called the initial side of the angle. The other ray is called the terminal side of the angle. This angle is said to be in standard position. |
 |
|
An angle can also be described in terms of rotation. Consider a point on the initial side of an angle. In order to get to the corresponding point on the terminal side of the angle and keep the vertex fixed, rotate the initial side until it coincides with the terminal side. |
 |
There are two possible directions to take. The initial side could be rotated clockwise until it arrives at the terminal side, or the initial side could be rotated counterclockwise.
In the realm of mathematics, rotations are typically counterclockwise. A counterclockwise rotation is called a positive rotation, and the corresponding angle has a positive measure. A clockwise rotation is called a negative rotation, and the corresponding angle has a negative measure.
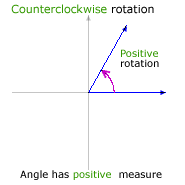 |
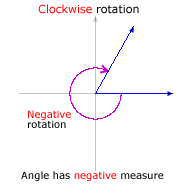 |
A circle has 360 degrees. For a rotation of 360°, the terminal side and the initial side of the angle coincide.
Here are illustrations of some selected angles described in terms of rotation:
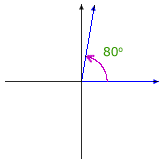 |
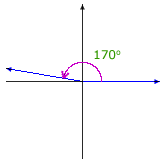 |
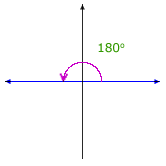 |
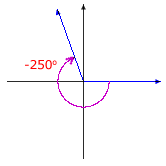 |
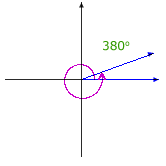 |
 |
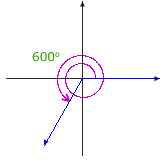 |
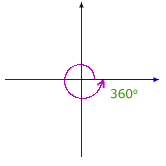 |
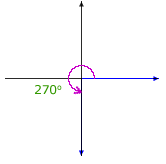 |
The same angle may be described as a rotation in many ways.
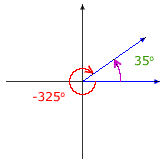
The angle pictured can be described as a rotation of 35° or a rotation of –325°. Furthermore, since a complete rotation has 360 degrees, the angle can also be described as a rotation of 35° + 360° = 395°, or 35° + 2(360°) = 755°, or 35° – 2(360°) = –685°, and so on.
Adding or subtracting a multiple of 360° to a rotation results in the same angle in standard position. A given angle in standard position has an associated family of infinitely many rotations, and the measures of any two rotations in the family differ by a multiple of 360°. The members of the family are known as coterminal angles because they have the same terminal side even though their rotations have different measures.
Callout
Example II.A.1: Find two positive angles and two negative angles that are coterminal with the angle 160°.
Solution:
To find positive angles that are coterminal with 160°, add multiples of 360° to 160°:
One positive angle coterminal with 160° has measure 160° + 360° = 520°.
Another has measure 160° + 2(360°) = 880°.
To find negative angles that are coterminal with 160°, subtract multiples of 360° from 160°:
One negative angle coterminal with 160° has measure 160° – 360° = –200°.
Another negative angle coterminal with 160° has measure 160° – 2(360°) = –560°.
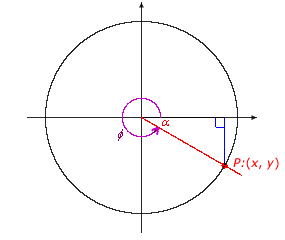
For any angle in standard position that is not a multiple of 90°, it is possible to draw an associated right triangle called a reference triangle. The reference triangle is used to define trigonometric function values for the angle.
To determine the reference triangle, follow these steps:
Callout
Example II.B.1: Given an angle of 30°, draw the reference triangle and find the trigonometric function values sin 30°, cos 30°, and tan 30°.
Solution:
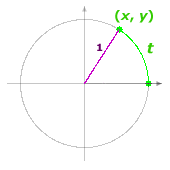
Place the 30° angle in standard position. |
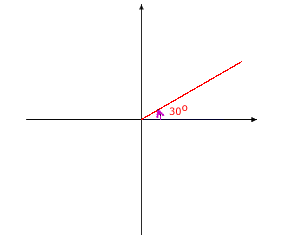 |
Recall the 1- Draw a circle of radius 2, and then draw the legs of the reference triangle. |
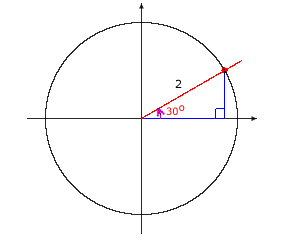 |
For a 1- The point P has coordinates (x, y) =
( Using the coordinates of the point P and the radius r:
|
|
Do the trigonometric function values depend on the size of the circle? What do you think?
Not surprisingly, the trigonometric function values of 30° found using the reference triangle approach do agree with the values determined in the previous section on right triangle trigonometry! However, as you will soon see, this new approach will allow to you to find trigonometric function values for angles that are not necessarily acute.
The 30° angle has its terminal side in the first quadrant. (See module 1, topic I-A for a review of the four quadrants.) The trigonometric functions of angles in other quadrants can be defined using the same process carried out for the 30° angle.
Trigonometric Functions of Any Angle
Suppose θ is an angle in standard position and P:(x, y) is a point on the terminal side, located a distance r from the origin. The trigonometric functions of the angle θ are defined in terms of x, y, and r:
The cosecant, secant, and cotangent of θ are the reciprocals of the sine, cosine, and tangent of θ, respectively.
To find the trigonometric function values of an angle with terminal side in quadrants II, III, or IV, create a reference triangle and determine the ratios. Be careful to note that x or y may be negative, depending on the quadrant. The value r is always positive because it is a measure of distance. Reference triangles associated with angles in quadrants II, III, and IV are shown below.
Angle θ in Quadrant II |
Angle θ in Quadrant I |
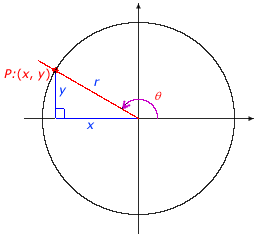 |
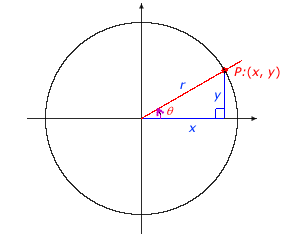 |
Angle θ in Quadrant III |
Angle θ in Quadrant IV |
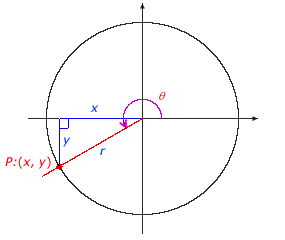 |
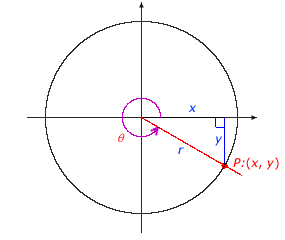 |
In practice, to find the trigonometric function values of a particular angle, start with either
- the measure of the angle
or
- a particular point P on the terminal side of the angle.
In example II.B.1, you were given the angle measure of 30° and then you determined the trigonometric function values. For each of the following examples, you will be given a point P on the terminal side of the angle.
Callout
Example II.B.2: Suppose that the point (-1, 1) lies on the terminal side of an angle θ in standard position. Find the six trigonometric function values of the angle.
Callout
Example II.B.3: Suppose that the point (–1, –![]() ) lies on the terminal side of an angle θ in standard position. Find sin θ, cos θ, and tan θ.
) lies on the terminal side of an angle θ in standard position. Find sin θ, cos θ, and tan θ.
Callout
Example II.B.4: Suppose that the point (6, –8) lies on the terminal side of an angle θ in standard position. Find sin θ, cos θ, and tan θ.
As illustrated in the preceding examples, the signs of the trigonometric function values depend on the quadrant of the angle.
Focusing on the positive values, if you remember the sequence all-sin-tan-cos, then you can quickly recall how the positive values correspond to the quadrants. This is illustrated in the circle diagram below.
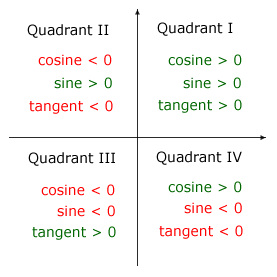 |
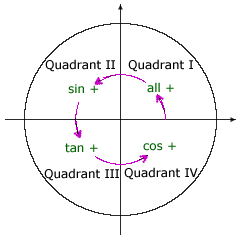 |
Coterminal Angles
If two angles are coterminal, then their trigonometric function values are the same, because the reference triangles are the same. For example, sin 30° = sin 390° = sin(–330°).
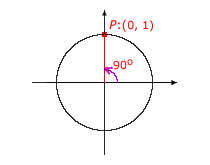
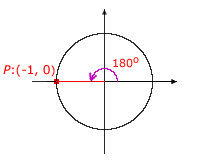
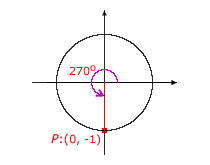
For the special cases where an angle is a multiple of 90°, there is no associated reference triangle. The definitions of the trigonometric functions still apply, but some of the trigonometric values are undefined, due to denominators that are equal to 0. The following table shows how to determine the values of the sine, cosine, and tangent for the angles of 0°, 90°, 180°, and 270°. In each case, the point P chosen on the terminal side of the angle is a point on the unit circle.
| Angle | Trigonometric Function Values |
|---|---|
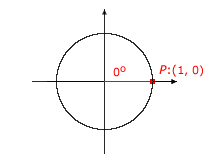 |
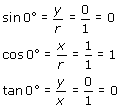 |
 |
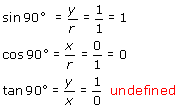 |
 |
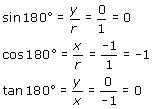 |
 |
 |
Recall that commonly occurring acute angles are 30°, 45°, and 60°. Commonly occurring angles between 0° and 360° include 30°, 45°, 60°, 120°, 135°, 150°, 210°, 225°, 240°, 300°, 315°, and 330°. Fortunately, if you know the trigonometric values for the acute angles, then by using symmetry, you can easily derive the exact trigonometric values for all of the angles on this list, without using a calculator!
Callout
Example II.D.1: Find sin 120° and tan 120°.
Solution:
120° is a quadrant II angle.
The reference triangle has a vertex at the origin.
The angle at that vertex is 180° – 120° = 60°. This acute angle is called the reference angle.

Reflect the reference triangle across the y-axis to get a triangle in the first quadrant.

The reference triangle associated with 120° is congruent to the quadrant I reference triangle associated with 60°. The trigonometric function values associated with the quadrant II triangle are the same as the values associated with the quadrant I triangle, except for possibly the signs.
In quadrant II, the sine is positive. Therefore, sin 120° = sin 60° =
![]() /2.
/2.
In quadrant II, the tangent is negative. Therefore, tan 120° = –tan 60° = –![]() .
.
The method used in this example relies on the idea of a reference angle.
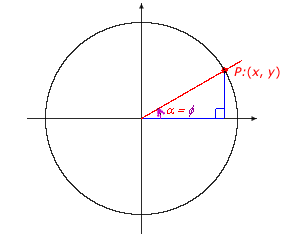
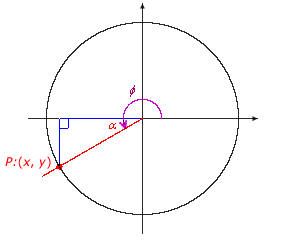
Reference Angle
Given an angle θ in standard position, find the associated acute angle ![]() formed by the terminal side and the x-axis. The angle
formed by the terminal side and the x-axis. The angle ![]() is called the reference angle. In the reference triangle associated with θ, the reference angle is the acute angle whose vertex is the origin.
is called the reference angle. In the reference triangle associated with θ, the reference angle is the acute angle whose vertex is the origin.
The reference triangle associated with angle θ is congruent to the quadrant I reference triangle associated with angle ![]() . The trigonometric function values of the angle θ are the same as the corresponding trigonometric function values of the angle
. The trigonometric function values of the angle θ are the same as the corresponding trigonometric function values of the angle ![]() , except for possibly the signs. The signs are determined by the quadrant of the angle θ.
, except for possibly the signs. The signs are determined by the quadrant of the angle θ.
Coterminal angles, since they have the same associated reference triangle, have the same reference angle. The calculation of the measure of the reference angle a depends upon the quadrant of the given angle, as summarized in the following table:
| Calculation of the Measure of the Reference Angle | |
|---|---|
Step 1: Given angle Step 2: Locate the quadrant associated with θ and
Step 3: Determine the reference angle |
|
Angles θ and |
Angles θ and
|
 Reference Angle |
 Reference Angle |
| Angles θ and
|
Angles θ and |
 Reference Angle |
 Reference Angle |
Callout
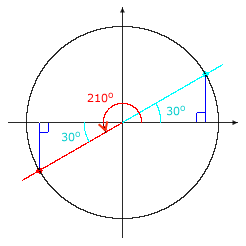
Example II.D.2: Find cos 210°.
Solution:
210° is a quadrant III angle whose measure is between 0° and 360°. Consulting the calculation table for a quadrant III angle, determine that the measure of the reference angle is 210° – 180° = 30°. |
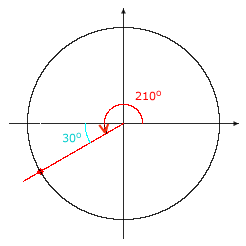 |
It is not imperative that you memorize the formulas for calculating the reference angle. You can draw the reference triangle associated with 210° and see that the acute angle at the origin in the triangle has measure 30°. The reference triangle associated with 210° is congruent to the quadrant I reference triangle associated with 30°, so the cosine of 210° must be the same as the cosine of 30°, except for possibly the sign. |
|
| In quadrant III, cosine is negative, so cos 210° = –cos 30° = – |
|
Callout
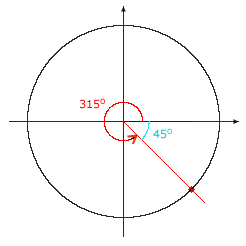
Example II.D.3: Find cos 1035°.
Solution:
First find an angle that is coterminal with 1035° and has measure between 0° and 360°.
Subtract 360° to get a coterminal angle: 1035° – 360° = 675° but is not between 0° and 360°.
Subtract 360° again: 675° – 360° = 315°.
315° is a quadrant IV angle that is coterminal with 1035° and has measure between 0° and 360°. Since 1035° and 315° are coterminal, cos 1035° = cos 315°. Consulting the calculation table for a quadrant IV angle, you'll find that the reference angle is 360° – 315° = 45°. |
 |
| It is not imperative that you memorize the formulas for calculating the reference angle. You can draw the reference triangle associated with 315° and see that the acute angle at the origin in the triangle has measure 45°. The reference triangle associated with 315° is congruent to the quadrant I reference triangle associated with 45°, so the cosine of 315° must be the same as the cosine of 45°, except for possibly the sign. | 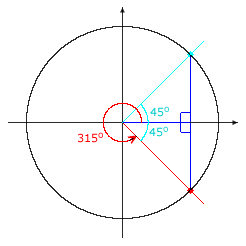 |
In quadrant IV, cosine is positive, so cos 1035° = cos 315° = cos 45° =
![]() /2.
/2.
After completing this section, you should be able to:
- convert between degree and radian measures
- understand the relationship between arc length and an angle measured in radians
- find linear speed and angular speed, and apply the relationship between them
In the discussion so far, angles have been measured in degrees. However, there is another system of measurement of angles, called radian measure, which proves to be especially convenient in scientific and mathematical settings.
The concept of a radian is related to the unit circle, the circle of radius 1 centered at the origin.
Since the circumference of a circle of radius π is 2πr, the circumference of the unit circle is 2π.
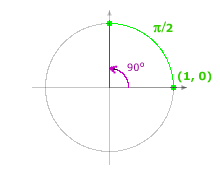
Suppose you walk counterclockwise on the unit circle, starting at the point (1, 0) on the positive x-axis. If you walk counterclockwise on the circle until you reach the positive y-axis, you will have traveled one-fourth of the circumference: a distance of 2π/4, or π/2. The path you have taken, the arc, corresponds to an angle of 90°. |
 |
| If you walk along the circle from the point (1, 0) to the negative x-axis, you will have traveled a distance of π (half of the circumference) and your arc of length π corresponds to an angle of 180°. | 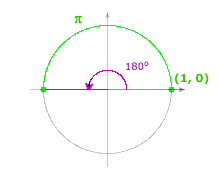 |
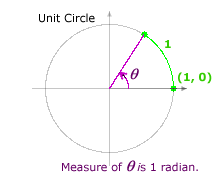
Now suppose you begin at the same starting point and travel a distance of 1 counterclockwise along the unit circle. Then, in radian measure, the corresponding angle is defined to be 1 radian. If you travel along an arc of length 2 on the unit circle, the corresponding angle is 2 radians. |
 |
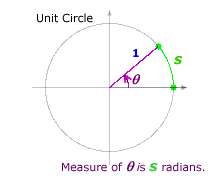
| The arc length s on the unit circle corresponds to an angle of s radians. |
 |
Traveling a distance π along the unit circle corresponds to the angle of π radians. Earlier, it was noted that a distance of π corresponds to the angle 180°. So, there is a simple relationship between radian measure and degree measure:
-
180° = π radians.
![]()
These equations can be used to convert units of measurement from degrees to radians, and from radians to degrees.
Callout
Example III.A.1: Convert 300° to radians.
Solution:
![]()
Callout
Example III.A.2: Convert –5π/4 radians to degrees.
Solution:
![]()
The following table lists the degree measure and the corresponding radian measure for a set of frequently used angles. The four background colors correspond to the four quadrants. The circle diagram illustrates the correspondence between degree measure and radian measure.
|
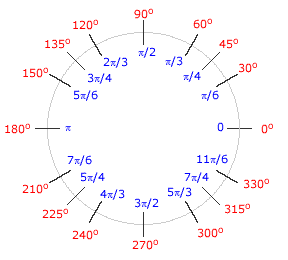 |
Considering that 180 degrees equals π radians, 360 degrees must then equal 2π radians. Recall that angles whose degree measures differ by an integer multiple of 360 degrees are coterminal. Therefore, angles whose radian measures differ by an integer multiple of 2π radians are coterminal, as well. Reference angles in radian measure are determined in an analogous fashion to reference angles in degree measure.
| Calculation of the Measure of the Reference Angle | ||
|---|---|---|
| Quadrant of Angle θ |
Measure of Reference Angle |
Measure of Reference Angle |
| I | |
|
| II | 180° – |
π – |
| III | |
|
| IV | 360° – |
2π
– |
Callout
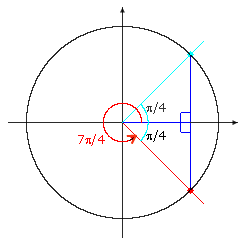
Example III.A.3: Find three angles that are coterminal with the angle of radian measure 15π/4 and determine the reference angle, also measured in radians.
Solution:
To find coterminal angles in radian measure, add or subtract multiples of 2π:
One coterminal angle has measure 15π/4 + 2π = 15π/4 + 8π/4 = 23π/4.
Another coterminal angle has measure 15π/4 – 2π = 15π/4 – 8π/4 = 7π/4.
Yet another coterminal angle has measure 15π/4 – 3(2π) = 15π/4 – 24π/4 = –9π/4.
There are infinitely many possible answers.
To find the reference angle, first find a coterminal angle whose measure is between 0 and 2π. The coterminal angle 7π/4 qualifies. Note that 7π/4 is a quadrant IV angle. The reference angle is 2π – 7π/4 = 8π/4 – 7π/4 = π/4.
A sketch of the associated reference triangle can be used to aid in finding the reference angle.
In the discussion so far, the focus has been placed on the unit circle. Similar ideas can be extended to any circle of radius r centered at the origin.
For angle
θ, let
s be the corresponding length of the arc on the circle of radius
r.
Let s' be the length of the corresponding arc on the unit circle.
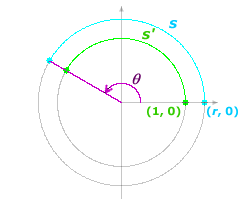
The ratio of the arc lengths s and s' is the same as the ratio of the radius r and 1.
That is,
![]() .
.
On the unit circle, the length of the arc s' is the measure of the angle θ in radians. In other words, s' = θ.
Therefore,
![]() ; equivalently,
; equivalently,
![]() .
.
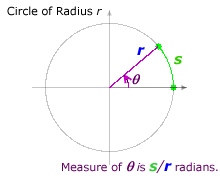
Radian Measure
For a circle of radius r with arc of length s and corresponding angle θ, θ = s/r in radian measure.
Equivalently, s = rθ, for θ measured in radians.
Callout
Example III.A.4: For a circle of radius 4 centimeters, find the length of the arc corresponding to an angle of 5π/6 radians.
Solution:
s = rθ = 4(5π/6) = 10π/3 centimeters, approximately 10.47 centimeters.
From this point forward, when an angle measurement is stated and no units are given, it is assumed that the measurement is in radians.
When considering applied problems, the concept of speed often arises. For example, a car might travel a linear speed of 55 miles per hour. A tire might achieve an angular speed of 200 revolutions per minute, or 400π radians per minute.
-
The linear speed, v, is equal to the distance traveled, s, divided by the time elapsed, t: v = s/t.
The angular speed, traditionally denoted by a lowercase omega, or
![]() , is equal to the angle of
rotation,
θ, divided by the time elapsed, t:
, is equal to the angle of
rotation,
θ, divided by the time elapsed, t:
![]() =
θ/t.
=
θ/t.
Suppose you are sitting on a rotating disk, such as a merry-go-round. |
 |
Regardless of where you sit on the disk, you will be traveling at the same angular speed, since all points on the disk will complete a 360° (or 2π radian) rotation in the same time. However, if you sit nearer the edge of the disk than the center, your linear speed will be greater. A point near the edge lies on a circle of greater radius than a point near the center. In one second, you will travel the same proportion of the circumference for either circle, but because the larger circle has a greater circumference, the distance traveled in that time will be greater, leading to a greater linear speed.
For angles measured in radians, there is a simple relationship between linear speed and
angular speed. Suppose a point is located r units from the center of rotation and an arc of
length s has been traversed in time t. Since s = rθ, linear speed =
v = s/t = rθ/t =
r![]() , where
, where
![]() is the angular speed, measured in radians per time unit.
is the angular speed, measured in radians per time unit.
-
Linear speed v and angular speed
![]() are related by
v = r
are related by
v = r![]() .
.
To apply this relationship, be careful to make sure your units are consistent. The units of
distance for v and r must be the same, the units of time for v and
![]() must be the same.
must be the same.
Callout
Example III.B.1: If a merry-go-round of radius 12 feet makes one complete rotation in 15 seconds, what is the linear speed of an individual riding on the merry-go-round 2 feet from the edge?
Solution:
The angular speed is
![]() .
.
Since the radius of the merry-go-round is 12 feet, an individual 2 feet from the edge must be 10 feet from the center.
For a point on a circle of radius 10 feet, the linear speed, v, is calculated:
![]()
The individual is traveling at a linear speed of approximately 4.2 feet per second.
After completing this section, you should be able to:
- find trigonometric function values for any real number
- graph the trigonometric functions and analyze their properties
At the beginning of this module, when we were focusing on the properties of right triangles, trigonometric function values were defined for acute angles. Next, by looking at angles in standard position, as rotations, the definitions of trigonometric functions were extended to apply to any angle. Then angles in radian measure were discussed.
This topic will extend definitions of trigonometric functions again, so that they are defined for all real numbers, rather than just for angles.
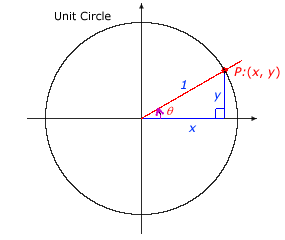
Take a look at the unit circle. For an angle θ and the associated point P:(x, y) on the unit circle:
That is, the x-coordinate of the point is the cosine of the angle, and the y-coordinate is the sine of the angle. x = cos θ and y = sin θ |
 |
The following table summarizes trigonometric function values for certain special angles, listed in both degree and radian measure.
| Angle θ | sin θ | cos θ | tan θ |
|---|---|---|---|
| 0° or 0 | 0 | 1 | 0 |
| 30° or π/6 |
|
|
|
| 45° or π/4 |
|
|
1 |
| 60° or π/3 |
|
|
|
| 90° or π/2 | 1 | 0 | undefined |
For every real number t, it is possible to assign corresponding values sin t and cos t.
If t is nonnegative, start at the point (1, 0) on the unit circle and mark off a distance t along the circle in the positive (counterclockwise) direction. Label the endpoint of the arc (x, y). Since the circle has radius 1, the arc of length t is equal to the angle rotation θ in radians. That is, t = θ. Define sin t = sin θ = y and cos t = cos θ = x. |
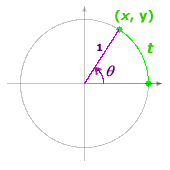 |
If t is negative, apply the same ideas, but travel in the negative (clockwise) direction.
Because of the link with the unit circle, trigonometric functions of real numbers are often called circular functions.
| Circular Functions (Trigonometric Functions of Real Numbers) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||
Callout
Example IV.A.1: Given t = π/3, what are the coordinates of the corresponding point (x, y) on the unit circle?
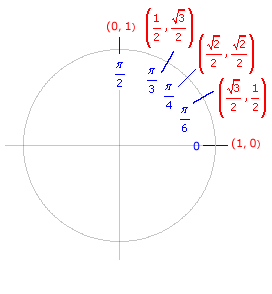
The first three columns of the table at the beginning of this topic can be transformed to the terminology of circular functions by substituting t = θ, x = cos θ, and y = sin θ, and writing the columns in order by t, x, and y. The transformed table is shown below. The diagram to the right visually displays this information on the unit circle.
| Real Value |
Point (x, y) on the Unit Circle |
 |
|
|---|---|---|---|
| t | x = cos t | y = sin t | |
| 0 | 1 | 0 | |
| π/6 |
|
|
|
| π/4 |
|
|
|
| π/3 |
|
|
|
| π/2 | 0 | 1 | |
Callout
Example IV.A.2: Given t = 5π/3, what are the coordinates of the corresponding point (x, y) on the unit circle?
The Sine Function
To get a feel for the graph of the sine function, make a table of values of the sine function and plot the values.
|
|
y = sin t
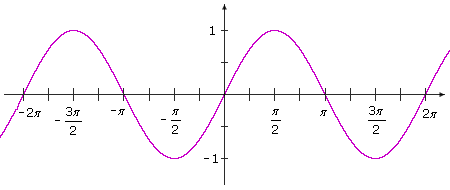
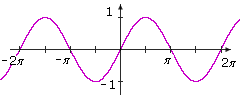
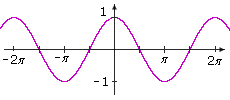
The graph of the sine function has many interesting features.
The graph oscillates between –1 and 1. According to the definition of the sine function, any real number may be input for t, so the domain of the sine function is (–∞ , ∞). The range is [–1, 1]. The graph crosses the t-axis at each integer multiple of π, so the zeros of the sine function are 0, ±π, ±2π, ±3π, ….
Trace the graph, starting at the origin. When t = 0, the y value is 0. As t increases, the y values increase until a peak of 1 is reached when t = π/2. Then as t goes from π/2 to 3π/2, the y values decrease to –1. As t goes from 3π/2 to 2π, the y values increase to 0.
If you make a copy of the curve from 0 to 2π and place it on top of the curve from –2π to 0, the two curves coincide. The graph has a pattern that repeats.
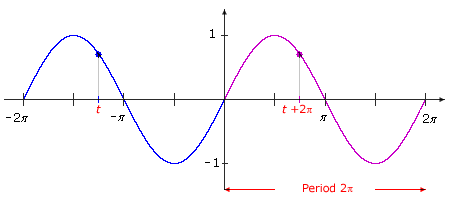
For any value of t, sin(t + 2π) = sin t. The sine function is said to be periodic with period 2π.
Periodic Function
If the graph of a function has a repeating pattern, the function is said to be periodic.
More precisely, a function f is called periodic if there is a positive constant p such that
f(t + p) = f(t) for all t in the domain of f. The period p of the function is the smallest positive constant for which f(t + p) = f(t) for all t in the domain.
Recall from college algebra that the graph of y = f(t + p) is a horizontal shift of the graph of y = f(t). (See module 1, topic III.)
If you shift the graph of y = f(t) to the left by p units, you arrive at the graph of y = f(t + p).
Saying that f(t + p) is equal to f(t) means that if you shift the graph of f to the left by p units, the graph remains the same.
In the case of the sine function, if you shift the graph of the sine function to the left by 2π, the graph is the same. If you shift the graph of the sine function to the left by less than 2π, the graph does not remain the same. The sine function is periodic with period 2π.
Alternatively, note that t and t + 2π correspond to coterminal angles, and coterminal angles have the same trigonometric function values. Therefore, sin(t + 2π) = sin t, and the sine function is periodic with p = 2π.
Given a periodic function, there are two measurements of particular interest: how often the graph repeats (the period) and how much the graph oscillates vertically (the amplitude).
Amplitude
Given a periodic function having a maximum and a minimum, the amplitude is defined to be half of the distance between the maximum and minimum y values.
Amplitude = ![]()
In the case of the sine function, the amplitude is
![]() |1 – (–1)| = 1.
|1 – (–1)| = 1.
Recall that graphs may exhibit certain types of symmetry. Take a careful look at the graph of the sine function and notice that it is symmetric with respect to the origin. (See module 1, topic III.) A function f whose graph is symmetric with respect to the origin is called an odd function, and such a graph satisfies f(–t) = –f(t). Therefore, sin(–t) = –sin t.
The Cosine Function
The cosine function can be graphed by using the same approach as the sine function:
|
|
y = cos t
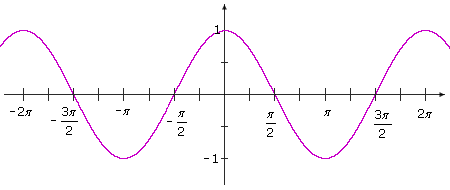
The graph oscillates between –1 and 1. The domain is (–∞ , ∞) and the range is [–1, 1].
The graph crosses the t-axis at
![]() , so the zeros of the cosine function are
, so the zeros of the cosine function are
![]() .
.
Trace the graph, starting when t = 0 and y = 1. As t increases, the y values decrease from the peak of 1 to –1 when t = π. Then as t goes from π to 2π, the y values increase to 1 again.
The cosine function is also periodic with period 2π and has an amplitude of 1. Notice that the cosine graph is symmetric with respect to the y-axis. A function f whose graph is symmetric with respect to the y-axis is called an even function, and satisfies f(–t) = f(t). Therefore, cos(–t) = cos t.
If you shift the cosine graph to the right by π/2, you arrive at the sine graph. Therefore, cos(t – π/2) = sin t. |
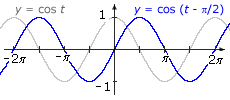 |
Here is a side-by-side comparison of the graphs of sine and cosine: |
|
| Sine Function | Cosine Function |
|
|
Domain: (–∞ , ∞) Periodic with period 2π |
Domain: (–∞ , ∞) |
The Tangent Function
The domain of a function of the form
![]() consists of those inputs
t in the domains of both
p and q
for which q(t) is nonzero.
consists of those inputs
t in the domains of both
p and q
for which q(t) is nonzero.
Recalling the definitions of the circular functions, since y = sin t,
x = cos t, and
tan t =
![]() when
x ≠ 0, the tangent function is defined as tan t =
when
x ≠ 0, the tangent function is defined as tan t =![]() , when cos t ≠ 0.
, when cos t ≠ 0.
The domain of the sine and cosine functions consists of all real numbers, and by examination of graph
of the cosine function, we can see that cos t = 0 when
![]() .
.
Therefore, the domain of the tangent function consists of all real numbers except
![]() .
.
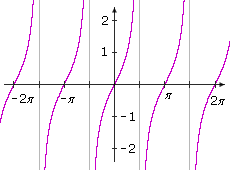
Vertical asymptotes occur at the t values for which the denominator cos t is zero. (See module 1, topic II-F for a review of asymptotes.)
|
|
y = tan t

The tangent function has period π. The graph has infinitely many vertical asymptotes. The function has no maximum or minimum, and so the amplitude is not defined. The range is (–∞, ∞).
The graphs of the cotangent, secant, and cosecant functions can be determined using the same approach. Here is a visual comparison:
Tangent Function |
Cotangent Function |
 |
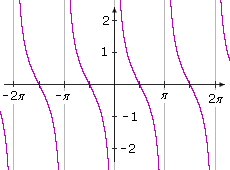 |
Domain: Range: (–∞ , ∞) |
Domain: Range: (–∞ , ∞) |
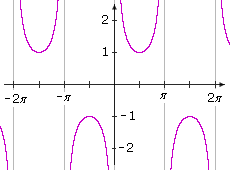
Cosecant Function |
Secant Function |
Domain: Range: (–∞ , –1] Since the sine is between –1 and 1 and the cosecant is the reciprocal of the sine, the cosecant must be greater than or equal to 1, or less than or equal to –1. The graph is periodic with period 2π. |
Domain: Range: (–∞ , –1] Since the cosine is between –1, and 1 and the secant is the reciprocal of the sine, the secant must greater than or equal to 1, or less than or equal to –1. The graph is periodic with period 2π. |
After completing this section, you should be able to:
- graph transformations of sine and cosine functions
Trigonometric functions such as sine and cosine can be thought of as building blocks for other functions. The graph of a trigonometric function may be transformed by horizontal and vertical translation, reflection, vertical stretching and shrinking, and horizontal stretching and shrinking.
If you are not well acquainted with transformations of functions, it is worth reviewing module 1, topic III-B. Use the table of transformations in module 1 as a reference as you consider transformations of sine and cosine.
The ultimate goal of this topic is to graph functions of the forms
y = A sin(Bt – C) + D and y = A cos(Bt – C) + D
and to analyze their characteristics.
To get a feel for the transformations of the sine function, start by considering simple functions.
Throughout the following examples, let |
 |
Callout
Example V.1: Graph g(t) = sin t + D.
Solution:
g(t) = sin t + D = f(t) + D
Each of the y-coordinates for g equals the sum of the y-coordinate for f and the constant D.
Here are some illustrations:
D > 0
Shift upward by 0.5. |
D < 0
Shift downward by 2. |
If D is positive, the graph of g is a shift of the graph of f upward by D units. If D is negative, the graph shifts downward by |D| units. Note that the amplitude and the period of the transformation are the same as those for the original graph. The amplitude is not the maximum y value. |
|
Callout
Example V.2: Graph h(t) = sin(t – C).
Solution:
h(t) = sin (t – C) = f(t – C)
If C is positive, the graph of h is a shift of the graph of f to the right by C units. If C is negative, the graph shifts to the left by |C| units. The value C is called the phase shift. Here are some illustrations:
C > 0
Shift to the right by π/4. |
C < 0
Shift to the left by π/3. |
Note that the amplitude and the period of the transformation are the same as those for the original sine graph.
Callout
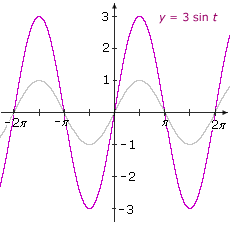
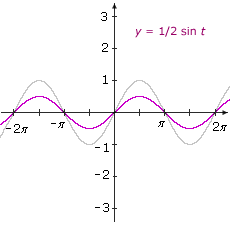
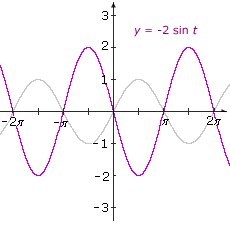
Example V.3: Graph p(t) = A sin t.
Solution:
p(t) = A sin t = f(t)
Each of the y-coordinates for p consists of the y-coordinate for f multiplied by the constant A.
Here are some illustrations:
|A| > 1
|
|A| < 1
|
Vertical stretching by a factor of 3. |
Vertical shrinking by a factor of 0.5. |
A < 0
Vertical stretching by a factor of 2 and reflection across the t-axis. Summary: If |A| > 1, the graph is stretched vertically. |
|
Callout
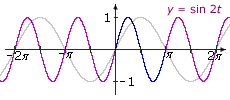
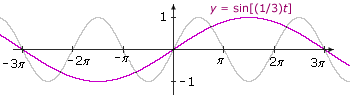
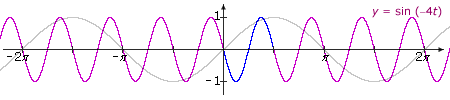
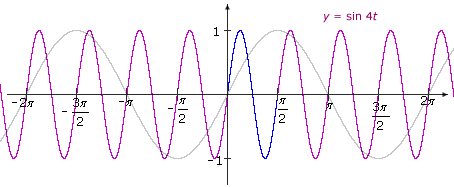
Example V.4: Graph q(t) = sin Bt. Solution: q(t) = sin Bt = f(Bt) The graph of q is a horizontal stretching/shrinking of the graph of f by a factor |B|. If B is negative, the graph is reflected across the y-axis. Here are some illustrations:
|
||
|
|B| > 1 and B < 0
The graph of y = sin 4t is a horizontal shrinking of y = sin t by a factor of 4; thus, the graph oscillates 4 times as fast as sin t. The graph of y = sin(–4t) is a reflection of the graph of y = sin 4t across the y-axis. In other words, since the sine function is odd, y = sin(–4t) = –sin(4t). One cycle is illustrated in blue. Period = 2π/4 = π/2. Summary: If |B| > 1, the function oscillates more rapidly than the graph of the original function. If |B| < 1, the function oscillates more slowly. If B is negative, the graph is reflected across the y-axis. The amplitude remains the same. The period of the transformation is 2π/|B|. |
Now consider several more complicated examples which involve a sequence of transformations.
Callout
Example V.5: Graph the function g(t) = 2 sin 3t – 1.
Solution:
The idea is to start with f(t) = sin t and arrive at g(t) via a sequence of transformations.
Notice that g(t) = 2 f(3t) – 1.
The graph of y = f(3t) = sin 3t is a horizontal shrinking of the graph of the sine function by a factor of 3. The resulting function has amplitude 1 and period 2π/3.

Next, find the graph of y = 2 f(3t) = 2 sin 3t. Take the graph of y = sin 3t and stretch it vertically by a factor of 2. The new graph has amplitude 2 and period 2π/3.
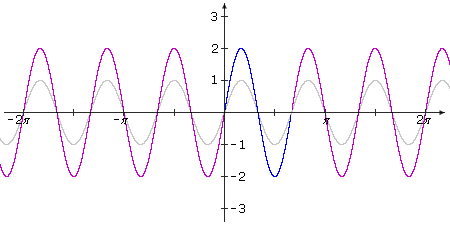
Lastly, determine the graph of y = 2 f(3t) – 1 = 2 sin 3t – 1. Take the previous graph and shift it downward by 1 unit. The final graph still has amplitude 2 and period 2π/3.

Callout
Example V.6: Graph the function h(t) = sin(4t – π).
Solution:
This function is complicated to graph because it involves two transformations in the horizontal direction: a horizontal shrinking and a horizontal shift.
Because the function f(t) = sin t completes one cycle for 0 ≤ t ≤ 2π, we know that
h(t) = sin(4t – π) completes one cycle for 0 ≤ 4t – π ≤ 2π.
| Solve for t: | 0 ≤ 4t – π ≤ 2π π ≤ 4t ≤ 3π π/4 ≤ t ≤ 3π/4 |
The period is 3π/4 – π/4 = 2π/4 = π/2.
Since the cycle starts at π/4 rather than 0, there is a horizontal shift to the right by π/4.
These facts can also be determined as a result of manipulating the formula for the function.
Notice that h(t) = sin(4t – π) = sin[4(t – π/4)].
Due to the factor of 4 in sin[4(t – π/4)], the period shrinks by a factor of 4 to 2π/4 = π/2.
The expression (t – π/4) indicates that there is a phase shift of π/4.
Perform the horizontal shrinking first to get
Then shift to the right by π/4:

The final graph has amplitude 1, period π/2, and phase shift π/4.
You now have all of the knowledge necessary to graph functions of the form y = A sin(Bt – C) + D.
In preparing a graph, be careful to first write the expression in the form y = A sin[B(t – C/B)] + D.
Graphing Functions of the Form y = A sin[B(t – C/B)] + D
To graph the function y = A sin[B(t – C/B)] + D, perform the following steps in the order given:
Stretch/shrink the graph of y = sin t horizontally to get the graph of y = sin Bt. The new graph has period 2π/|B|. If B < 0, also reflect the graph across the y-axis.
Shift the graph of y = sin Bt horizontally by C/B to get the graph of y = sin[B(t – C/B)]. The new graph has phase shift C/B.
Stretch/shrink the graph of y = sin[B(t – C/B)] vertically to get the graph of y = A sin[B(t – C/B)]. If A < 0, also reflect the graph across the t-axis. The new graph has amplitude |A|.
Shift the graph of y = A sin[B(t – C/B)] vertically to get the graph of y = A sin[B(t – C/B)] + D.
The resulting graph is a transformed graph of y = sin t, having amplitude |A|, period 2π/|B| and phase shift C/B.
The same steps apply for graphing a function of the form y = A cos(Bt – C) + D.
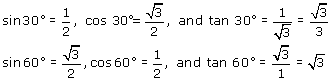

 [1, ∞)
[1, ∞)